SwinTransformer: Hierarchical Vision Transformer using Shifted Windows
- 提出了一个Hierarchical 架构的Transformer,让patch大小从小到大进行增加。为了减少计算cost,transformer的计算只在每一个window里面进行,并且为了消除只在window进行self-attention的操作,提出了使用shift-win的操作方式,让不同patch能够不局限于当前相邻的win分块。
- 提出了一种Hierarchical transformer, 每一层的patch大小不同,每一层会融合相邻patch得到一个更大的patch。
- 提出了一种win-shift方式,让网络的关注不limit到固定win中。
- 主要区别如文章teaser所示:

Method
输入图像首先进行patch partition, 每个patch大小是 $4 \times 4$ 大小,经过线性映射后输入到transformer中。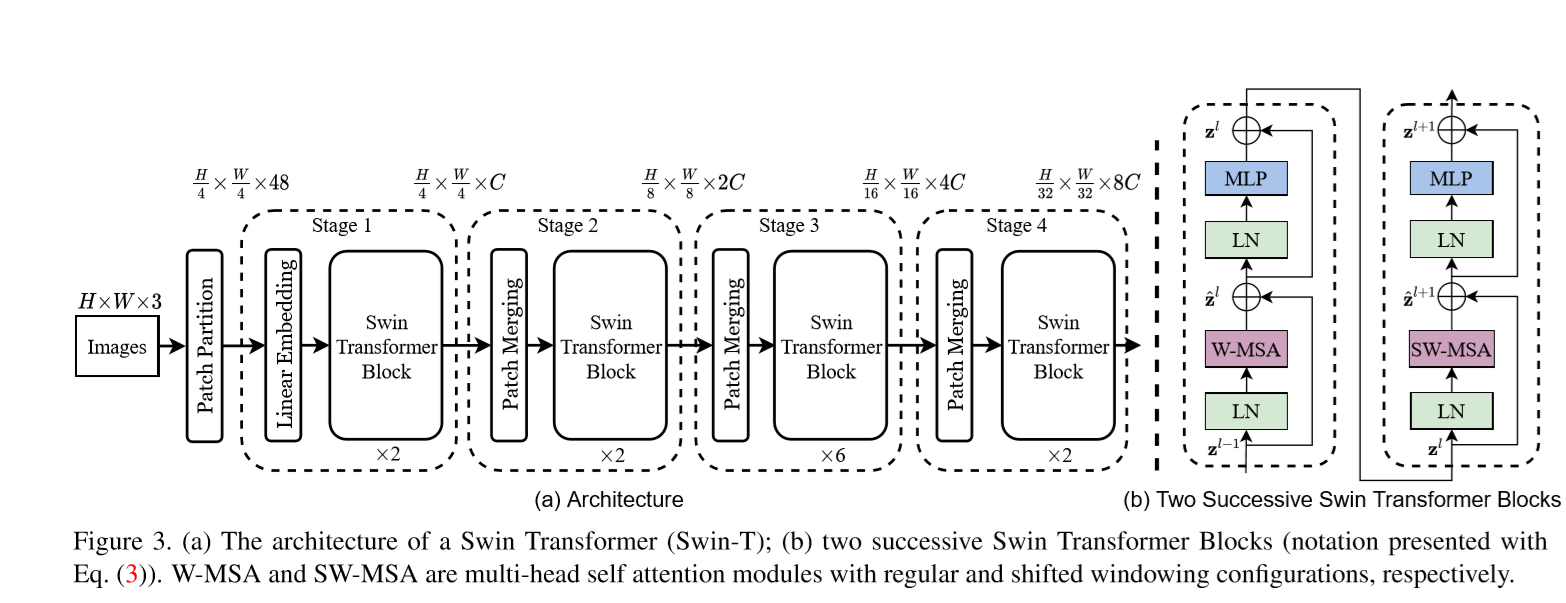
奇数层的Transformer 中的win不进行偏移(对应shift_size=0),每一个patch在win内部做self-attention。
Shift Win
具体的将原来的图像feat.进行roll 操作,然后取win。这样每一个win所用于计算attention的patch就不局限与之前的win。增加了transformer的感受野。
After this shift,a batched window may be composed of several sub-windows that are not adjacent in the feature map, so a masking mechanism is employed to limit self-attention computation to within each sub-window.

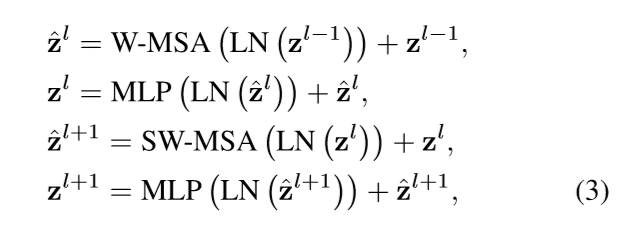
Code Analysis
Framework:
- patch_embed(x) 将 img embed 到特征空间,
- 然后 layers 依次过 BasicLayer ,最后实现分类
1 | class SwinTransformer(nn.Module): |
PatchEmbed:
首先是对 patch 的 embed ,patch 之间没有重叠
self.proj = nn.Conv2d(in_chans, embed_dim, kernel_size=patch_size, stride=patch_size)其次是对 window 进行位置编码,每一个 window 不同
1
2self.absolute_pos_embed = nn.Parameter(torch.zeros(1, num_patches, embed_dim))
trunc_normal_(self.absolute_pos_embed, std=.02)值得注意的是,
x = self.proj(x).flatten(2).transpose(1, 2) # B Ph*Pw C在之后的传播都是基于 token 来进行传播的,token [1, 96]。有 Ph * Pw 个token 这里 x 是 [B, H/4* W/4, C]
SwinTransformerBlock:
对于任意一个输入 feature
先对其划分 window :
x_windows = window_partition(shifted_x, self.window_size); self.window_size=7得到nW*B, window_size, window_size, C的输出。每一个 window 都被放在了 batch 中因为他们会经过相同的处理。如果
self.shift_size即 window 需要偏移,那么需要对特征图 x 进行 roll 处理。并且在__init__中构 maks:作者在偶数层 SwinTransformerBlock 中会 roll 一次。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20if self.shift_size > 0:
# calculate attention mask for SW-MSA
H, W = self.input_resolution
img_mask = torch.zeros((1, H, W, 1)) # 1 H W 1
h_slices = (slice(0, -self.window_size),
slice(-self.window_size, -self.shift_size),
slice(-self.shift_size, None))
w_slices = (slice(0, -self.window_size),
slice(-self.window_size, -self.shift_size),
slice(-self.shift_size, None))
cnt = 0
for h in h_slices:
for w in w_slices:
img_mask[:, h, w, :] = cnt
cnt += 1
mask_windows = window_partition(img_mask, self.window_size) # nW, window_size, window_size, 1
mask_windows = mask_windows.view(-1, self.window_size * self.window_size)
attn_mask = mask_windows.unsqueeze(1) - mask_windows.unsqueeze(2)
attn_mask = attn_mask.masked_fill(attn_mask != 0, float(-100.0)).masked_fill(attn_mask == 0, float(0.0))下一步就是将一个 window 中的所有值都换成列向量
x_windows = nW*B, window_size*window_size, C然后对该向量做 attention,相当于 window 中每一个点做attention。最后将特征还原
1 | def forward(self, x): |
WindowAttention:
qkv 计算:输出 channel 大小为3倍,对应了不同的 qkv
1
self.qkv = nn.Linear(dim, dim * 3, bias=qkv_bias)
计算,dim 中包含了 num_heads 的分组。
1
2qkv = self.qkv(x).reshape(B_, N, 3, self.num_heads, C // self.num_heads).permute(2, 0, 3, 1, 4)
q, k, v = qkv[0], qkv[1], qkv[2]multi-head
attn=[-1, 3, 49, 49]q=[-1, 3, 49, 32]1
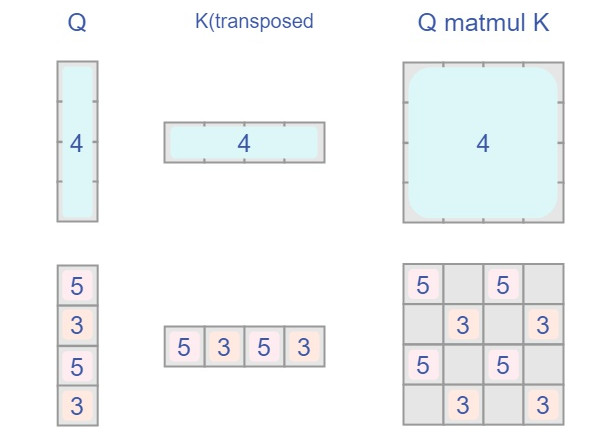
attn = (q @ k.transpose(-2, -1))
高维矩阵乘法:知乎
两个高维矩阵@
a:shape=[2,2,3]和b:shape=[2,3,2]计算的时候把 a 的第一个 shape=[2,3] 的矩阵和 b 的第一个 shape=[3,2] 的矩阵相乘,得到的shape=[2,2],同理,再把 a,b 的第二个 shape=[2,3] 的矩阵相乘,得到的 shape=[2,2] 。 最终把结果堆叠在一起,就是2个 shape=[2,2] 的矩阵堆叠在一起
Attention Mask:
仅仅使用固定模式的 window, 缺少了 window 与 window 之间的相关性,作者提出使用 shifted window partitioning 。当使用 shift window 操作的时候,需要计算 attention mask 来进行对 attention 的修改。知乎
为什么需要 maks 对 attention 进行修改 ?

window的个数翻倍了,由原本四个窗口变成了9个窗口。而作者并没有区别地去实现 9 窗的代码,而是利用了 mask 来进行 对 方式一 得到的 attn 进行再处理最终得到 方式二的每一个 window 的 attention。(注意图方式中,红色框内部计算 self attention)
我们需要计算每个块中的 self attention (块0, 块1 …..) 最直接的方式是把每一个不同大小的块 (window) 给 partitioning 出来,然后计算。但是每个块所含的pixel 数量不同,这无法并行。于是采用方式二。

先对原 feature 进行 roll 操作得到图右边的样式。然后依旧计算
2x2的 window 的 self attention对于 4号 window,其计算的就是其本身的self attention,不用改变,
对于 5,3号 window,我们之前计算了该合并窗口 (5,3 所组成的那个 1/4 窗口) 但是需要的其实是 5、3号内部的 S.A. 对于该窗口而言,我们已得到两两之间的attention,但是我们只需要各自内部 (inner 5, inner 3) 的不需要交叉的 (inter 5,3) 。所以