Self-Supervised Denoise Method:

Introduction

使用noise 和cln作为GT的图像训练对比较难获得，延长曝光时间多次拍摄得到的AVE cln img也不一定是很好的cln GT，这种拍摄困难，要求拍摄主体不移动(人像眨眼睛，颤抖等)，在某些情况下在实验环境可以获得，但是对于wild img是不好实现的。

基于以上的观点，提出了只给noise img然后进行去噪。在理论上进行论证可以参考章节： Noise2Noise: Learning Image Restoration without Clean Data 的原理以及公式推导部分。

在N2N中，主要假设为： $\mathbb{E}{ x + n’ } = \mathbb{E}{ x + n’’ } = x $ 其中 $x$ 为不可获得的干净图片。基于次假设可以推出：

$\argmin_{\theta} \mathbb{E_{y|x}}\{\mathcal{L} (f_{\theta}(y), x)\} = \argmin_{\theta} \mathbb{E_{y|x}}\{\mathcal{L} (f_{\theta}(y), z)\}$

其中， $y = x + n’, z = x + n’’$, $ \mathcal{L} $ 是 $L_2$ 损失。换句话说，在这条件下，要想网络tends to output the $ \mathbb{E}{x}$ ，理论上可以证明上面两个损失函数都可以，故，在我们没有GT时，采用第二个损失也是可以的。

在Nei2Nei中，主要假设为： $\mathbb{E}{ y } = x; \mathbb{E}{ z } = x + \epsilon $ 其中 $x$ 为不可获得的干净图片; $ \mathbb{E}{y} \neq \mathbb{E}{z}, y; z$ 是对于同一个sence的真实抽样(抖动，遮挡，光照变化)。基于次假设可以推出：

$\mathbb{E_{y,z|x}}\{||f_{\theta}(y)-x||_2^2\} = \mathbb{E_{y,z|x}}\{||f_{\theta}(y)-z||_2^2\} - \sigma^2(\hat{y}_i) + 2\epsilon \mathbb{E_{y,z|x}}\{(f_{\theta}(y) -x)^T\}$

Motivation

Discovery 1:

不论是N2N还是Nei2Nei还是其他的去噪方法考虑的是加性噪声： $y = x + n$, 其中 $x$ 是GT无噪声图， $n$ 是加性噪声。如果考虑到ISP的非线性操作，在基于N2N 这类self-supervised training 方法中影响到了其basic 假设即： $\mathbb{E}{ x + n’ } = \mathbb{E}{ x + n’’ } = x $ 。我们实际采样到的图片是 $x + n’$ 进过ISP (非线性操作)后的图片即: $x’ = ISP(x+n’)$ 而N2N based method 都直接在 $x’$ domain中假设加性噪声期望等于0，但是实际上 $n’$ 在进过 $ISP(\cdot)$ 这种spatial-correlation 非线性操作后，其噪声没有了噪声空间无关性，换句话说噪声变得depend on the spatial，尽管原来的 $\mathbb{E}{x + n’} = x$ 在进过ISP处理后， $\mathbb{E}{ISP(x + n’)} \neq x$.

Discovery 2:

As demonstrated in Nei2Nei, 我们无法没差别地进行 scenes 一致并且 noise independent 的两次抽样。所有原来假设我们更倾向于Nei2Nei的推导结果，那么怎么去生成 $x+n’$ 和 $x+n’’$ 成为了本文的关键。

Summery：

[x] 考虑ISP的非线性变化，我们得到的img不是直接的img与加性噪声的和， $\mathbb{E}{ISP(x + n’)} \neq x$.
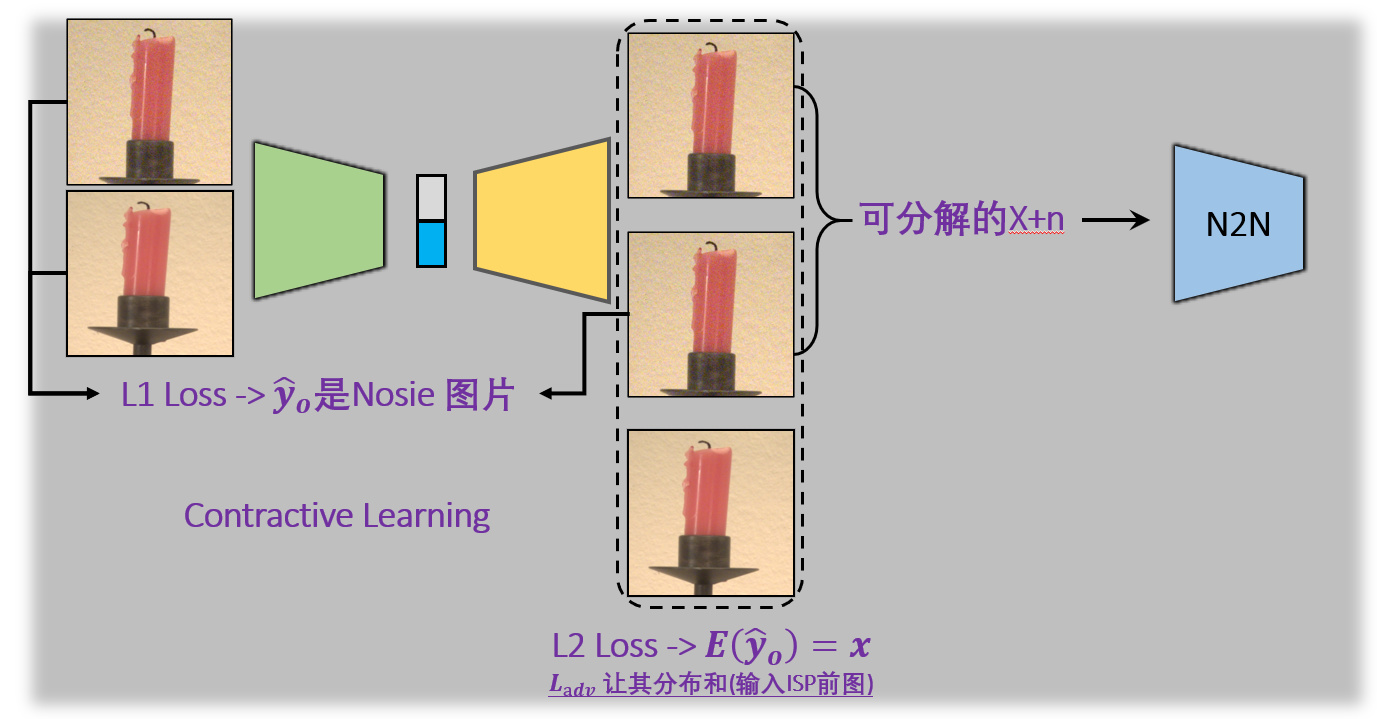
[x] 我们需要构造 $x+n’$ 和 $x+n’’$ ，使用NN去拟合 $ISP^{-1}(\cdot)$ 将我们得到的图片逆投影原加性噪声图像的空间中，然后用生成的图片pair (完全满足N2N的假设：无抖动，无光照差…) 去train N2N网络。

Method

生成噪声图，Inverse the ISP processing. 构建一个NN去生成满足N2N条件的数据对。进行训练。
在测试的时候，只用输入噪声图，加上不同的噪声，生成不同的加性域的 $x+n’$ 和 $x+n’’$ ，输入到N2N网络中进行去噪。
image|690x360