去噪论文阅读-6

Posted on

Attention 在去噪中的理解：

在刷比赛的时候，我发现很多方法没有Unet的范化性高(在所有数据集都有很好的结果)。其中实验了一些关于attention的模型，主要的改进是在Unet的上菜样的过程中加入attention的模块。

  • 为什么在上采样阶段使用Attention而不是在下采样or Both？
    这样做是考虑到，网络在下采样阶段是来采集提取图像的特征的，使用卷积+感受野已经可以对特征有很好的提取效果了，我觉得Attention的作用主要在于特征的融合以及特征的refine。至于使用Attention对特征的提取是否比Conv更好，就目前来说，我不是很清楚。在上采样的时候就是图像利用学到的特征解决任务的过程，这时使用Attention在直觉上是make sense的。

怎么理解Attention去噪：

  • 一类attention: $C \times (HW)$ 求自相关性得到 $ \bm{Mat} \in HW \times HW$ 再乘与原feature map. 代表为：Non Local, Self Attention等。
    这个问题和程深讨论了一下，也学习到了很多，总结如下：
    对比NLM(None Local Mean)方法，网络将相似的patch进行平均，得到最终的去噪结果。同理，我们在feature作attention的时候，对每一个position而言，我们计算他与其他位置的C维特征的相似度，即类比与NLM中找相似度高的patch. 当将attention计算得到的关系矩阵乘回feature map的时候，我们只让相似度高的特征点的特征向后传播。进行后面的融合操作，即类比于NLM中在相似度高的patch中取ave的操作(在NN中可以有ave也有其他的融合)。

  • 一类是使用GAP， GMP得到channel或者spatio的feature map然后在这上面使用sigmoid函数得到mask，乘于原feature map。代表为Dual Attention, Shuffle Attention, SE Net等。
    从两方面来解释这个attention的作用：

    • Channel attention: 对每个channel的feature 进行GAP得到在 $C_i$ 的特征在整个 $HW$ 的平均值，通过这样的方式可以看出哪一个feature对于整体的激励大(重要性高)从而将激活高的特征维度的到的特征往下传播。
    • Spatial attention: 对feature map在 Channel维度上进行GAP 或者GMP得到 $H \times W$ 的feature, 再使用sigmoid得到mask。考虑一个位置上的特征点，综合其所有特征，在conv filter的感受野下，该位置上的特征是否比其他位置上的特征重要，如果某位置上存在比较重要的特征，就往后传播。

SA-NET: SHUFFLE ATTENTION FOR DEEP CONVOLUTIONAL NEURAL NETWORKS

文章目的是减少网络的计算量。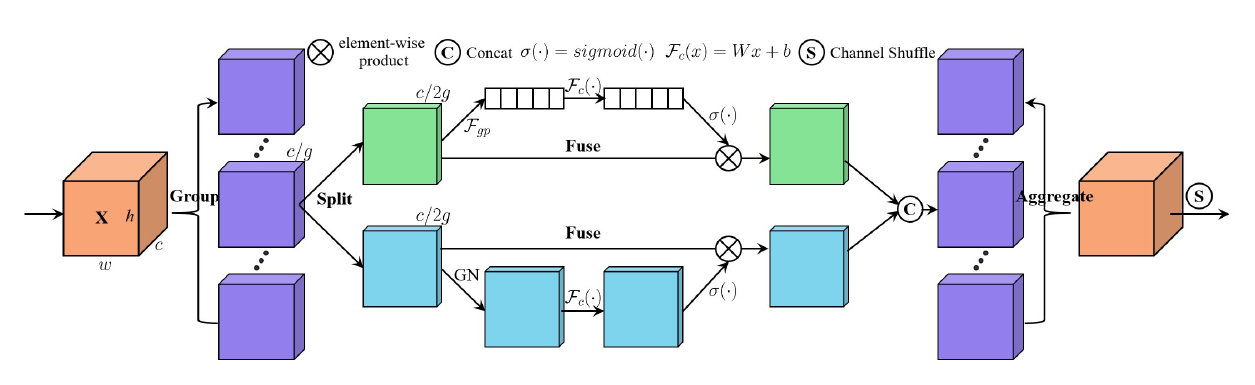
image|690x211 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
class sa_layer(nn.Module):
    """Constructs a Channel Spatial Group module.
    Args:
        k_size: Adaptive selection of kernel size
    """

    def __init__(self, channel, groups=64):
        super(sa_layer, self).__init__()
        self.groups = groups
        self.avg_pool = nn.AdaptiveAvgPool2d(1)
        self.cweight = Parameter(torch.zeros(1, channel // (2 * groups), 1, 1))
        self.cbias = Parameter(torch.ones(1, channel // (2 * groups), 1, 1))
        self.sweight = Parameter(torch.zeros(1, channel // (2 * groups), 1, 1))
        self.sbias = Parameter(torch.ones(1, channel // (2 * groups), 1, 1))

        self.sigmoid = nn.Sigmoid()
        self.gn = nn.GroupNorm(channel // (2 * groups), channel // (2 * groups))

    @staticmethod
    def channel_shuffle(x, groups):
        b, c, h, w = x.shape

        x = x.reshape(b, groups, -1, h, w)
        x = x.permute(0, 2, 1, 3, 4)

        # flatten
        x = x.reshape(b, -1, h, w)

        return x

    def forward(self, x):
        b, c, h, w = x.shape

        x = x.reshape(b * self.groups, -1, h, w)
        x_0, x_1 = x.chunk(2, dim=1)

        # channel attention
        xn = self.avg_pool(x_0)
        xn = self.cweight * xn + self.cbias
        xn = x_0 * self.sigmoid(xn)

        # spatial attention
        xs = self.gn(x_1)
        xs = self.sweight * xs + self.sbias
        xs = x_1 * self.sigmoid(xs)

        # concatenate along channel axis
        out = torch.cat([xn, xs], dim=1)
        out = out.reshape(b, -1, h, w)

        out = self.channel_shuffle(out, 2)
        return out

与之前不同的是：

  1. 在SA使用了Group Norm在代码中看来和INSNorm是一样的效果。
  2. 首先对feature map进行group，将其分为G个group然后在每个group中进行计算。
  3. CA、SA得到mask后，使用了 $W_i \in \mathbb{R}^{C/2G\times 1 \times 1}; R_i \in \mathbb{R}^{C/2G\times 1 \times 1}$ 作为weight 和bias。这两个是可训练的参数。初始化为0,1.

感觉文章没什么创新点。