去噪论文阅读-2-Self Supervised

导言：这篇文章两篇论文，Self Supervised去噪相关。

Neighbor2Neighbor: Self-Supervised Denoising from Single Noisy Images

时间线：

• Noise2Noise
• Probabilistic Noise2Void
• Noise2Void_ICCV2019
• Noise2Self_ICML2019
• Self-Guided_ICCV2019
• Noisier2Noise_CVPR2020
• Self2Self_CVPR2020

What is the problem

1. 噪声对不好获取
2. self的方法没有很好利用独立噪声的信息。

   The requirement of large amounts of noisy-clean image pairs for supervision limits the wide use of these models
   Existing self-supervised denoising approaches suffer from inefficient network training, loss of useful information, or dependence on noise modeling.

3. 不同与Noise2Noise，this paper 假设两张noise 图片的期望并不相同。
   

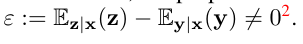
   The ground-truths of two noisy observations are difficult to be the same due to occlusion, motion, and lighting variation

Method

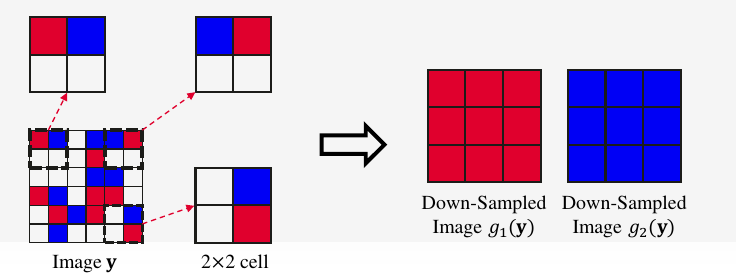
1. pipeline
   
2. 抽样方法：随机抽cell中的邻近对(4选2)，一个抽为 $g_1(y)$ 一个抽为 $g_2(y)$ (2选1)。
   
3. loss
   

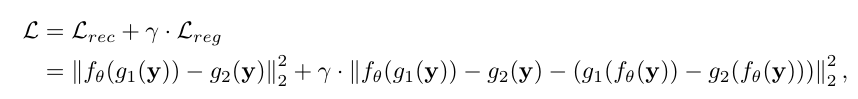
Noise2Noise: Learning Image Restoration without Clean Data

Why it works?

1. 疑问：
   • 输入是一张噪声图，GT也是一张噪声图，怎么学到cln的img？
   • 网络如何学习

一些理解

参考理解

噪声是随机的，目标是constant不变的，就像估计room的温度，每一次估计值都是充满噪声的(不精确)但是我们需要的仅仅是测完(看完)所有测试温度 ${T_1, T_2 … T_n}$ 后取其均值作为我们的最终估量值。类比于img 去噪过程。本身而言，我们取得无噪声图像GT时就是一次噪声平均值，我们只是把它当作了无噪声的img。倘若网络学习的东西并不是我们所认为的 $nosie \rightarrow cln$ 的点到点mapping，而是keep 变化中需要保留的content呢？

具体来说，由于噪声是不稳定的，随机的，当网络将噪声图 $N_1$ 映射至 $N_2$ 时，要让总体的 $\mathcal{L} = \mathbb{E}{ L(N_1, N_2) } $ 最小，抛去无法降低的loss，随机的噪声，网络只能让img中不变的地方保持或者更加清晰才能使得loss下降。

原理以及公式推导

对于一次估计而言: $\argmin_{\theta} \mathbb{E_y} \{\mathcal{L} (f_{\theta}(z), y)\}$ ，我们想让每一次预测值 $f_{\theta(z)}$ 与观测到的采样值 $y = {y_1, y_2, ..., y_n}$ 尽可能相近。也就是让其损失期望最小。一般而言我们采用L2损失，这样对 $\mathcal{L} (f_{\theta}(z), y)$ 求z的偏导，得到 $z = \mathbb{E_y}{y}$ 时最小。

对于 $\forall x, y,z$ ，其中 $x$ 是理想无噪声图片GT， $y, z$ 都是同一场景不同噪声的采样的图片。去噪过程中我们的目标函数为：

$$\argmin_{\theta} \mathbb{E_{y|x}}\{\mathcal{L} (f_{\theta}(y), x)\} = \argmin_{\theta} \mathbb{E_{y,z|x}}\{||f_{\theta}(y)-x||_2^2\} = \argmin_{\theta} \mathbb{E_{y,z|x}}\{||f_{\theta}(y)+z-z-x||_2^2\}$$

而其中

$$\mathbb{E_{y,z|x}}\{||f_{\theta}(y)+z-z-x||_2^2\} = \mathbb{E_{y,z|x}}\{||f_{\theta}(y) - z||_2^2\} + \mathbb{E_{y,z|x}}\{||z-x||_2^2\} + 2\mathbb{E_{y,z|x}}\{f_{(\theta}(y)-z)^T(z-x)\}$$

• 其中 $\mathbb{E_{y,z|x}}\{||z-x||_2^2\}$

图片中的公式(8)的 $\hat{y_i}$ 是噪声图，所以可以得到 $\mathbb{E_{y,z|x}}\{||z-x||_2^2\} = \sigma^2(\hat{y_i})$

• 其中 $2\mathbb{E_{y,z|x}}\{(f_{\theta}(y)-z)^T(z-x)\}$ 中， $(f_{\theta}(y)-z)^T$ 与 $(z-x)$ 不独立 无法进行计算，

进一步我们将其化为：

$$2\mathbb{E_{y,z|x}}\{(f_{\theta}(y)-z +x -x)^T(z-x)\} = 2\mathbb{E_{y,z|x}}\{(f_{\theta}(y) -x)^T(z-x) + (z-x)^T(x -z)\}$$

其中

$$\mathbb{E_{y,z|x}}\{ (z-x)^T(x -z) \} = Cov\{(x-z)^T,(z-x)\} + \mathbb{E}\{(x-z)^T\} \mathbb{E}\{(z-x)\}$$ $$Cov\{(x-z)^T,(z-x)\} = -D(x-z) \\ = - (\mathbb{E}_{z,y|x}\{x-z\}^2 - \mathbb{E}_{z,y|x}\{ E^2(x-z) \})$$

所以：

$$Cov\{(x-z)^T,(z-x)\} + \mathbb{E}\{(x-z)^T\} \mathbb{E}\{(z-x)\} \\ = - (\mathbb{E}_{z,y|x}\{x-z\}^2 - \mathbb{E}_{z,y|x}\{ E^2(x-z) \}) - \mathbb{E}^2\{(z-x)\} \\ = -\mathbb{E}_{z,y|x}\{x-z\}^2$$

在Noise2Noise中 $ \mathbb{E}(x) = \mathbb{E}(z)$ 所以 :

$$\mathbb{E_{y,z|x}}\{||f_{\theta}(y)-x||_2^2\} = \mathbb{E_{y,z|x}}\{||f_{\theta}(y)-z||_2^2\}$$

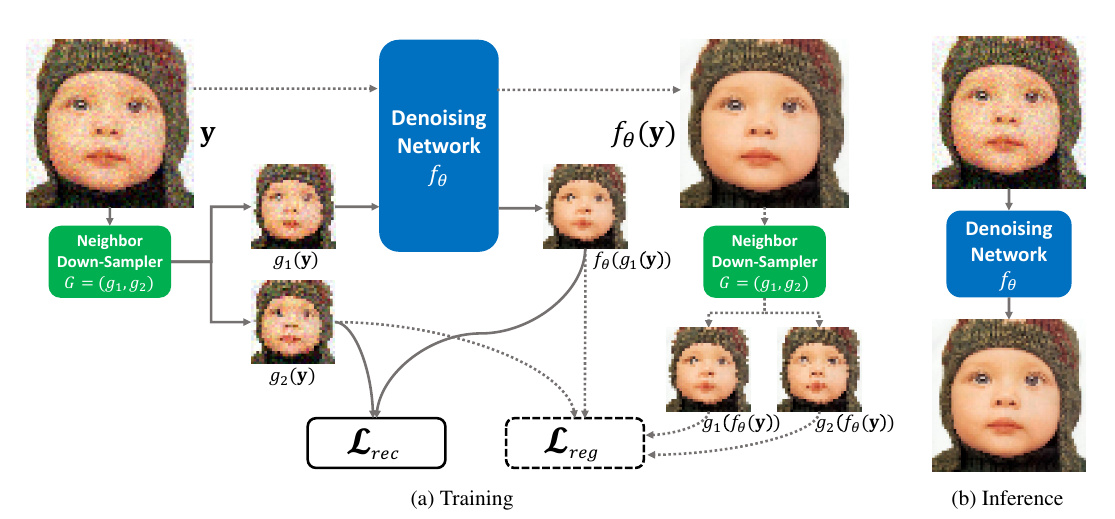
在Neiber2Neiber中 $\mathbb{E}(x) \neq \mathbb{E}(z)$ 所以

$$\mathbb{E_{y,z|x}}\{||f_{\theta}(y)-x||_2^2\} = \mathbb{E_{y,z|x}}\{||f_{\theta}(y)-z||_2^2\} - \sigma^2(\hat{y}_i) + 2\mathbb{E_{y,z|x}}\{(f_{\theta}(y) -x)^T(z-x)$$

这样就可以获得论文中的(10)-(11):