去噪论文阅读-7

Practical Deep Raw Image Denoising on Mobile Devices

Pipeline

在真是情况中，ISO在拍摄的时候会自动变化，不同的ISO引起的噪声的分布不同，本文Proposed to 提供一个ISO blind 的去噪网络，值得注意的是，网络本身是train在ISO-indpendent的数据上，网络不是blind，方法流程blind。

In real applications the camera will automatically adjust the ISO settings according to the scene illumination, thus one has to consider different noise levels when training the denoising neural network. A straightforward solution is to train a single network to cover a wide range of ISO settings, but it puts extra burden on the network itself as the noise variation in the training data becomes quite large.

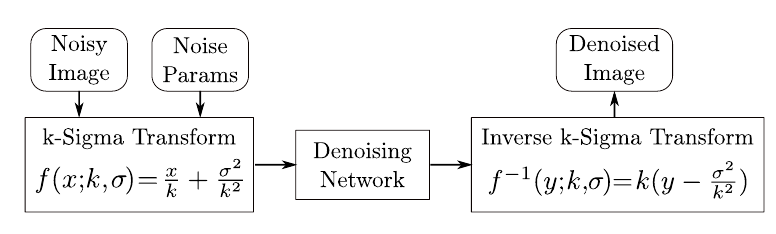
针对不同的ISO，使用K-Sigma 变化将raw 图像转为ISO-independent的数据输入到网络中。 $x = f(x^;k,\sigma)$ 其中 $x^$ 是sensor得到的raw图， $x$ 是转换后的数据。 在 $x$ 域中进行去噪，然后使用ISO-dependent的转换函数 $f^{-1}(x; k, \sigma)$ 可以将去噪后的图片转回原ISO对应的图像。

Why noise is ISO-dependent?

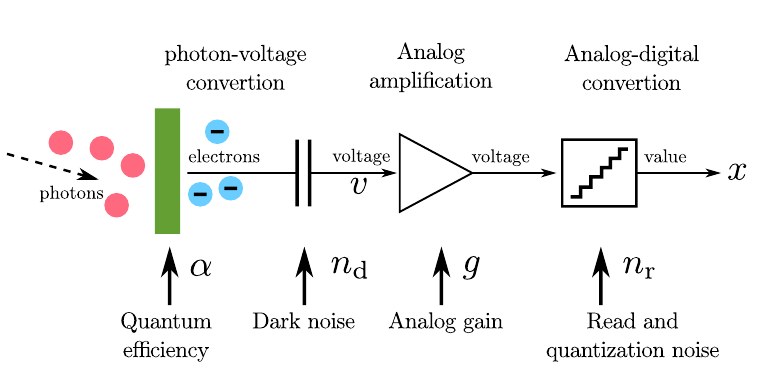
我们从sensor得到的图像 $x^$ 在理想状态下经过光量子收集( $u^$ )+模拟增益，得到实际数字信号的 $x$ .但是这个过程中往往存在Noise，我们实际得到的图像可以建模为:

$$x = g(\alpha u + n_d) + n_r$$

其中， $n_d; n_r$ 是在各个阶段加入的噪声， $u$ 是光量子的接受量， $u \sim \mathcal{P}(u^*)$ , 进一步可以得到：

$$x \sim (g\alpha)\mathcal{P}(\frac{x^*}{g\alpha}) + \mathcal{N}(0, \sigma^2) \\ \mathbb{E}(\mathcal{P}(X)) = X \\ Var(\mathcal{P}(X)) = X$$

泊松分布的期望方差 $g\alpha = k $ 。可以得到

$$\mathbb{E}(x) = x^* \\ Var(x) = kx^* + \sigma^2$$

推导：

$$x \sim k\mathcal{P}(\frac{x^*}{k}) + \mathcal{N}(0, \sigma^2) \\ \frac{x}{k} \sim \mathcal{P}(\frac{x^*}{k}) + \mathcal{N}(0, \frac{\sigma^2}{k^2}) \\ \frac{x}{k} + \frac{\sigma^2}{k^2} \sim \mathcal{P}(\frac{x^*}{k}) + \mathcal{N}(\frac{\sigma^2}{k^2}, \frac{\sigma^2}{k^2}) \\ \frac{x}{k} + \frac{\sigma^2}{k^2} \approx \mathcal{N}(\frac{x^*}{k}, \frac{x^*}{k}) + \mathcal{N}(\frac{\sigma^2}{k^2}, \frac{\sigma^2}{k^2}) \\ \frac{x}{k} + \frac{\sigma^2}{k^2} \approx \mathcal{N}(\frac{x^*}{k} + \frac{\sigma^2}{k^2}, \frac{x^*}{k} + \frac{\sigma^2}{k^2}) = \mathcal{N}(f(x^*), f(x^*)) \\ f(x) \sim \mathcal{N}(f(x^*), f(x^*))$$

$f(x)$ 的分布只和 $f(x^)$ 有关，我们可以使用 $f(x)$ 去预测 $f(\hat{x}^)$ 然后使用 $f^{-1}(\cdot)$ 来得到最终结果。

Network

网络的设计是针对mobile 来设计的，使用了separable-conv来减少计算量：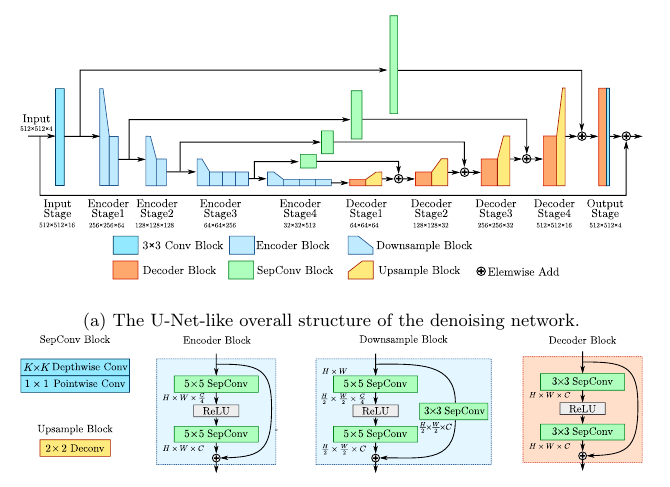

实验

对每一个ISO 都估计采样样本的方差和期望，使用

$$\mathbb{E}(x) = x^* \\ Var(x) = kx^* + \sigma^2$$

去拟合得到 $k; \sigma$ 的值。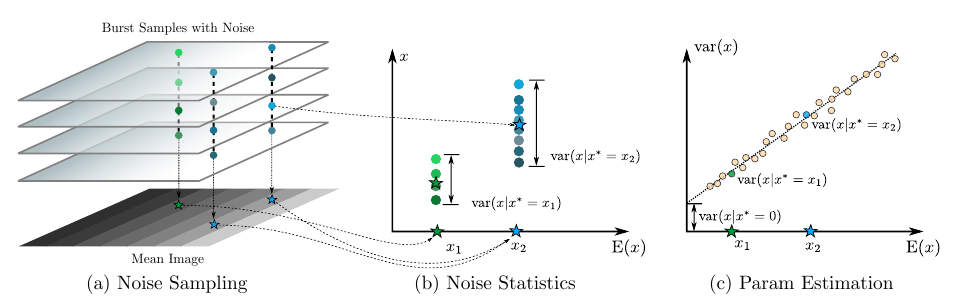


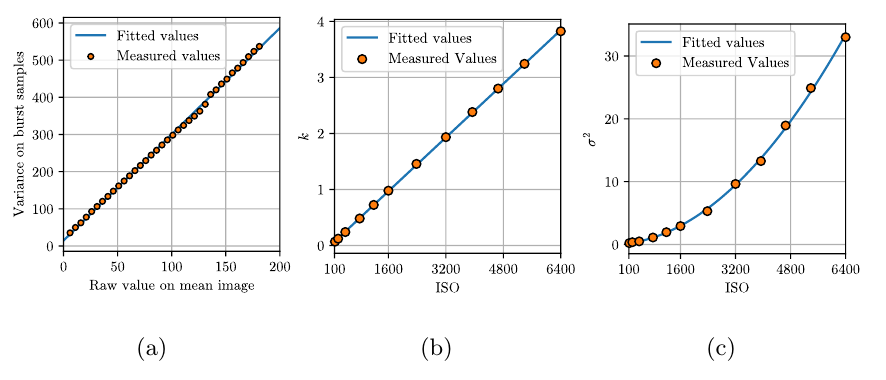
首先得到不同的ISO的采样结果，计算该手机的 $k;\sigma$ 然后使用 k-sigma变化 $ f(x) = \frac{x}{k} + \frac{\sigma^2}{k^2}$ 得到转换后的图片，在这些图像中进行训练。换句话说，对于每个手机而言 $k; \sigma$ 是一样的， $k; \sigma$ 是同一个手机通过在不同ISO下的数据拟合得到的。然后对于所有数据集中的数据，可以任意变化、增强之，进行 k-sigma变化得到ISO-independent数据。作者假设不同的手机 $k; \sigma$, 没有对不同sensor进行实验。