导言：暑假老师叫我们做动作识别，在查阅了一些做Action Recognition的paper后发现18年AAAI上一篇St-gcn[Spatial Temporal Graph Convolutional Networks for Skeleton-Based Action Recognition]的性能和表现都不错而且是利用了我之前接触过的openPose的，加之采用的是之前没有学过的gcn来进行建模的，所以准备花一些时间对其进行学习。

这篇博客就是关于如何使用st-gcn来进行动作识别的。

OpenPose基础参考我这篇文章

1 论文framework

使用openPose对数据进行pose节点的预测
将pose节点构造成Graph
分别在时域、空间上进行GCN

2 论文特点

图卷积的应用
只使用人体节点来进行动作预测，使得模型范化能力、容错能力大大增加。但是我在学习这篇产生了一个疑问：
1. 先对视频进行skeleton的提取，然后只对节点数据进行train或者预测，这样虽说是有其优点，但是否会丢失色彩、环境、细节表达的信息呢？
2. 该流程并不符合端到端的性质，还需要借助一些pose的estimation才能进行，显得实用性不大。
基于视频的训练预测

3 GCN

一句话说就是input是一个图(Graph数据结构)的卷积

4 论文解读

5. Introduction

Among these modalities, dynamic human skeletons usually convey significant information that is complementary to others. However, the modeling of dynamic skeletons has received relatively less attention than that of appearance and optical flows.

其实在原文中作者就已经提出了我的疑问，但是他并没有说清楚两种方式到底谁更好一点，就我而言觉得使用appearance的flows更好一点，这里存疑。再学习了更多只是后我会继续审视这个问题。

5.1 早期的利用skeleton的动作识别

将每一帧的joint信息stack起来然后做成一个特征向量然后使用时域理论去的分析这些特征来分类视频。显然这样的预测没有显示地考虑到joint与joint之间的空间联系，这种联系在动作识别中是很重要的。

Earlier methods of using skeletons for action recognition simply employ the joint coordinates at individual time steps to form feature vectors, and apply temporal analysis thereon

所以作者提出了一种针对与两个维度的卷积来处理这种即在时间上有在空间上有关联性的数据。

6 Method

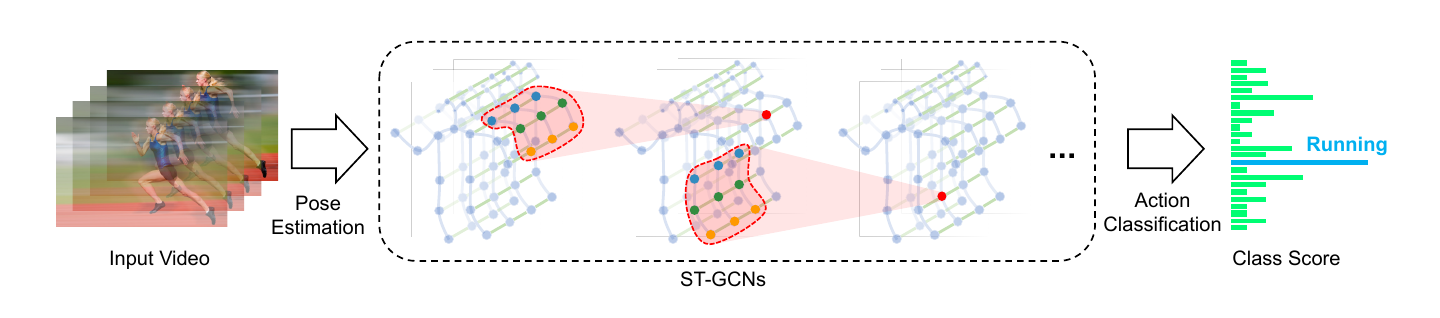
网络流程图

上面这张图很重要，整个paper的思路差不多都在这张图里面了。作者是如何联系上空间与时间的呢？在文章中时间空间维度主要是只卷积核的维度

在中CNN的卷积是针对图像的，其卷积核的两个维度(h,w)分别是卷积核的长、宽，只是像素值层面的意义，但是在stgcn中就不一样了，卷积核(G,K)一维是在空间维度，一维是在时间维度。paper中T取的9,K取的3。具体意义在之后会详细说。

6.1 时间维度

在时间的维度上作者参考以往的做法，将一个时间段的所有帧stack在一起，构成了input在时间维度上通道的宽度

6.2 空间维度

在同一个视频中，相邻帧的同一个joint是可以相互连通的，这样就构成了在空间维度上的桥梁。

其实上面两个老是说空间、时间维度会整得人头晕，实际上就是构建了一个图，这个图是由T个frames的skeleton组成的，而每一帧的相同的joint是连通的。

6.3 什么是时空域的图卷积

作者将这个问题与CNN做了一系列的对比，内容十分精彩。先是对CNN卷积公式的抽象：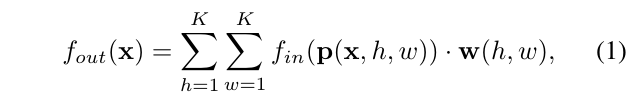

CNN卷积公式

其中p是抽样函数，而CNN中抽样就是将以卷积核大小的原始数据按行列顺序依次拿出。

where the sampling function emerates the neighbors of location x.

f(p(x,h,w))的意思就是取出p(x,h,w)这个位置的数据,w是每一个通道的权重

有了CNN的抽象公式，我们可以类比一下，确定一个CNN、GCN过程中其实只需确定两点：

怎么抽样？
权值怎么确定？

在CNN中这两个问题很明确：

按照卷积核大小依行、列顺序依次抽样
每一个抽样得到的数据有不同的权值，其值就是卷积和这个位置的值

那么这下类比到GCN中理解就很好理解了，我们只需要定义好我们的抽样函数，以及定义好对于每一类位置抽样出来的数据分配权值函数即可。

抽样函数的定义就体现了stgcn是如何做到空间、时间上的卷积的，作者拓展了卷积核2个维度的概念，一个维度作为时间上的长度，一个维度作为空间上的长度。那读者肯定会问什么是时间上的长度、什么是空间上的长度呢？它们数值又是多大呢？继续把这张图贴出来：

网络流程图

那个红色的区域就是一个stgcn的卷积核，它在时间维度中就是以目标中心点(红色点)为中心，左右相邻的T/2帧作为卷积核的一个维度，paper中取的9(注意要是奇数)，而蓝色、绿色、黄色对应了三个不同的权值，注意是3个不同的权值，不是9个，因为蓝色是一组，绿色是一组，黄色是一组这里会读者会感到与CNN矛盾的地方，其实不矛盾，在CNN中每一个抽样点单独为一个组，以3x3为例，9个点依次是一个独立的组，每个组的权值就是核上的该位置值的权值。

知道了stgcn的卷积核是什么，那怎么取值呢？在时域中我们简单地就可以将相邻帧取出来然后进行卷积，那权值函数我们怎么确定呢？具体来说，我们怎么将抽样的joints进行分组呢？

paper中提供了3个partion strategies.依次对应分1,2,3组。paper使用的是最后一种策略即分3组的策略。

Uni-labeling，全部B(vti)分为一个subset，但是这样会失去局部的特点属性。只需要将K = 1，且lti(vtj) = 0即可，这就表明了只有1个类，且所有vti的subset序号为0。
Distance partitioning 安装距离来分子集，分为root点和其他点。只需要将K = 2，且lti(vtj) = d(vtj,vti)即可，因为D=1,所以d()只能为0-1之间的两个值。
Spatial configuration partitioning 根据空间的分区。

作者基于body motion 可以被大致的分为近重心运动以及偏重心运动。所以将远离中心的节点分为一类，将近心的分为一类，根分为一类，一共三类。

1
2
3

l_ti(v_tj) = 0 if rj = ri 
		   = 1 if rj < ri # 近心点
		   = 2 if rj > ri # 远心点

r_i is the average distance from gravity center to joint i over all frames in the training set.

注意是该点所有帧的距离重心平均距离。

if layout == 'openpose':
    self.num_node = 18
    self_link = [(i, i) for i in range(self.num_node)]
    neighbor_link = [(4, 3), (3, 2), (7, 6), (6, 5), (13, 12), (12,
                                                                11),
                     (10, 9), (9, 8), (11, 5), (8, 2), (5, 1), (2, 1),
                     (0, 1), (15, 0), (14, 0), (17, 15), (16, 14)]
    self.edge = self_link + neighbor_link
    self.center = 1

从源码可以看出来center点是neck点。注意如果两点都邻接不可到中心点即距离都是inf，那么算作远心点

paper中使用的是邻接矩阵来表示距离。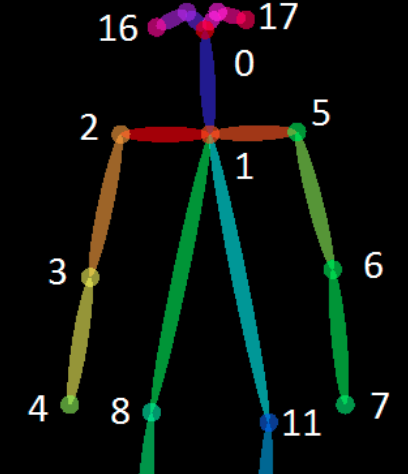
coco示意图

coco示意图

7 Graph的建立

该模块的代码主要在graph.py文件中，在这个模块主要分了3类：

邻接矩阵的建立
归一化以及快速图卷积的与处理
权值的分组

7.1 邻接矩阵的建立

这里采用的是OpenPose的节点进行举例，需要指出的是作者的节点连接顺序与本来OP中提供的输出格式的连接顺序是不同的，具体的体现在(2,8)(5,11)点的连接，这样的连接对结果没有影响，但是也不能简单地认为将OP中的节点pair改为st-gcn中的顺序就匹配了，因为不能忘记OP中的PAF的训练是按照(1,8)(1,11)进行训练的。

...
self.edge = self_link + neighbor_link
...
def get_hop_distance(num_node, edge, max_hop=1):
    A = np.zeros((num_node, num_node))
    for i, j in edge: #构建邻接矩阵
        A[j, i] = 1
        A[i, j] = 1
    # print(A)

    # compute hop steps
    hop_dis = np.zeros((num_node, num_node)) + np.inf
    transfer_mat = [np.linalg.matrix_power(A, d) for d in range(max_hop + 1)]

    # range -> [0,n)

    arrive_mat = (np.stack(transfer_mat) > 0) # transfer_mat是list类型，需要将list堆叠成一个数组才能进行>操作
    for d in range(max_hop, -1, -1):
        # print(arrive_mat[d])
        hop_dis[arrive_mat[d]] = d
    return hop_dis

7.1.1 np.linalg.matrix_power(matrix, expo)

方矩阵乘法.

expo > 0 进行matrix的连成。
exp0 = 0 对角矩阵
expo =-1 逆矩阵，
expo < 0 matrix(-expo),即 matrix × matrix × np.linalg.matrix_power(matrix, 2) = eyes()

上一段代码中获得了带自环的邻接矩阵，非连接处是inf。

7.2 归一化以及快速图卷积的与处理

def get_adjacency(self, strategy):
    valid_hop = range(0, self.max_hop + 1, self.dilation) # 合法的距离值：0或1
            adjacency = np.zeros((self.num_node, self.num_node))
            for hop in valid_hop:
                adjacency[self.hop_dis == hop] = 1 # 将0|1的位置置1,inf抛弃
            normalize_adjacency = normalize_digraph(adjacency)#图卷积的预处理
    ...
# 图卷积的预处理           
def normalize_digraph(A):
    Dl = np.sum(A, 0)  #计算邻接矩阵的度
    num_node = A.shape[0]
    Dn = np.zeros((num_node, num_node))
    for i in range(num_node):
        if Dl[i] > 0:
            Dn[i, i] = Dl[i]**(-1) #由每个点的度组成的对角矩阵
    AD = np.dot(A, Dn)
    return AD

D矩阵，在paper中是没有提到D矩阵的，只是提出了一种图卷积的公式，在后面会详细讲解。在这里只需要知道D是有i节点的度所组成的对角矩阵。然后使用的图卷积公式是$D^{-1}AX$

在预处理完成后，我们就需要对18个节点进行分组了，安装paper中的第3中分组方式分为3组：

elif strategy == 'spatial':
    A = []
    for hop in valid_hop:
        a_root = np.zeros((self.num_node, self.num_node))
        a_close = np.zeros((self.num_node, self.num_node))
        a_further = np.zeros((self.num_node, self.num_node))
        for i in range(self.num_node):
            for j in range(self.num_node):
                if self.hop_dis[j, i] == hop:
                    if self.hop_dis[j, self.center] == self.hop_dis[
                            i, self.center]:
                        a_root[j, i] = normalize_adjacency[j, i]
                    elif self.hop_dis[j, self.
                                      center] > self.hop_dis[i, self.
                                                             center]:
                        a_close[j, i] = normalize_adjacency[j, i]
                    else:
                        a_further[j, i] = normalize_adjacency[j, i]
        if hop == 0:
            A.append(a_root)
        else:
            A.append(a_root + a_close)
            A.append(a_further)
    A = np.stack(A)
    self.A = A

# st_gcn.py:
# A = torch.tensor(self.graph.A, dtype=torch.float32, requires_grad=False)
# self.register_buffer('A', A) 将A注册成寄存器变量

原理与6.3节中所讲的是一样的。需要特别指出的是，这里的normalize_adjacency已经是$D^{-1}A$了，而且将$D^{-1}A$得到的矩阵(shape = 18,18)分成了$\overline{A}$(shape = 3,18,18)分成了3组，后面也对应了3组不同的权值。到此图的建立已经完成。

7.2.1 Pytorch 中 register_buffer

注册变量,A是tensor变量。在之后的调用只用self.A_即可调用，寄存器变量访问快。

1	self.register_buffer('A_',A)

对于其他变量：
Pytorch参数其实包括2种。

一种是模型中各种 module含的参数，即nn.Parameter，我们当然可以在网络中定义其他的nn.Parameter参数;
另外一种是buffer。前者nn.Parameter中的参数每次optim.step会得到更新，而不会更新后者buffer。buffer的更新在forward中，optim.step只能更新nn.Parameter类型的参数。

这里还需要注意在st_gcn.py中，A是不会改变的常量，requires_grad=False

8 网络的输入

该模块的代码位于st_gcn,tgcn中。
整个网络的输入是一个(N = batch_size,C = 3,T = 300,V = 18,M = 2)的tensor所以在进行2维卷积(n,c,h,w)的时候需要将 N 与 M 合并起来形成(N * M, C, T, V)换成这样的格式就可以与2维卷积完全类比起来。CNN中核的两维对应的是(h,w)，而st-gcn的核对应的是(T,V).

...
def forward(self, x):

    # data normalization
    N, C, T, V, M = x.size()
    x = x.permute(0, 4, 3, 1, 2).contiguous()
    x = x.view(N * M, V * C, T)
    x = self.data_bn(x)
    x = x.view(N, M, V, C, T)
    x = x.permute(0, 1, 3, 4, 2).contiguous()
    x = x.view(N * M, C, T, V)
    ...

9 Model

Model的建立是这篇文章的主要重点，模型由3类层组成，其中层又有包含关系。注意在输入模型之前，是做了通道的变换处理的，上一节所示。(为了做成网络的输入格式:N C H W)，每一个st_gcn又包含了residual模块。

self.data_bn = nn.BatchNorm1d(in_channels * A.size(1))
self.st_gcn_networks = nn.ModuleList((
    st_gcn(in_channels, 64, kernel_size, 1, residual=False, **kwargs0),
    st_gcn(64, 64, kernel_size, 1, **kwargs),
    st_gcn(64, 64, kernel_size, 1, **kwargs),
    st_gcn(64, 64, kernel_size, 1, **kwargs),
    st_gcn(64, 128, kernel_size, 2, **kwargs),
    st_gcn(128, 128, kernel_size, 1, **kwargs),
    st_gcn(128, 128, kernel_size, 1, **kwargs),
    st_gcn(128, 256, kernel_size, 2, **kwargs),
    st_gcn(256, 256, kernel_size, 1, **kwargs),
    st_gcn(256, 256, kernel_size, 1, **kwargs),
))
# initialize parameters for edge importance weighting
if edge_importance_weighting:
    self.edge_importance = nn.ParameterList([
        nn.Parameter(torch.ones(self.A.size()))
        for i in self.st_gcn_networks
    ])
else:
    self.edge_importance = [1] * len(self.st_gcn_networks)
# fcn for prediction
self.fcn = nn.Conv2d(256, num_class, kernel_size=1)

可以看出模型是：

一个输入层的batchNorm(接受的通道数是in_channels#3 * A.size(1)#18 模型的输入是一个(N,C,T,V,M)的tensor，

N 视频个数
C = 3 (X,Y,S)代表一个点的信息(位置+预测的可能性)
T = 300一个视频的帧数paper规定是300帧，不足的重头循环，多的clip
V 18 根据不同的skeleton获得的节点数而定，coco是18个节点
M = 2 人数，paper中将人数限定在最大2个人

第二部分由10层st_gcn构成
最后加一层全连接层

每一层st-gcn是这样搭建的：

self.gcn = ConvTemporalGraphical(in_channels, out_channels,
                                         kernel_size[1])
# temporal
self.tcn = nn.Sequential(
    nn.BatchNorm2d(out_channels),
    nn.ReLU(inplace=True),
    nn.Conv2d(
        out_channels,
        out_channels,
        (kernel_size[0], 1),
        (stride, 1),
        padding,
    ),
    nn.BatchNorm2d(out_channels),
    nn.Dropout(dropout, inplace=True),
)

if not residual:
    self.residual = lambda x: 0

elif (in_channels == out_channels) and (stride == 1):
    self.residual = lambda x: x

else:
    self.residual = nn.Sequential(
        nn.Conv2d(
            in_channels,
            out_channels,
            kernel_size=1,
            stride=(stride, 1)),
        nn.BatchNorm2d(out_channels),
    )

self.relu = nn.ReLU(inplace=True)

paper中模型的阐述

作者貌似将第一层的st_gcn(in_channels, 64, kernel_size, 1, residual=False, **kwargs0)不算作stgcn模块中，所以一共有9层。每一个st-gcn层(这里不要把层和模型的名字搞混淆了)都用residual模块来改进。可以在源码中看出来当通道数要增加时，作者使用1x1conv来进行通道的翻倍，另外使用stride = 2来完成pool的效果使得长宽减半。这里埋个Residual Net的坑。

st-gcn层其实包含了两个主要的模块

对于spatial空间的 gcn：ConvTemporalGraphical模块
对于temporal空间的 tcn模块

前面总是将两个空间和着一块说，而且又将2维度与CNN中卷积核相类比，很容易将这里理解错误，st-gcn在卷积时其实是分开卷积的先卷spatial，再卷temporal，而这两维的合起来就是拓展意义上的卷积核，在实际操作中对于单一的一维(时间维或者空间维)是非开使用卷积核的2维的数据的。

self.gcn = ConvTemporalGraphical(in_channels, out_channels,kernel_size[1]) #使用卷积核的第二维即 3 组

self.tcn = nn.Sequential(
            nn.BatchNorm2d(out_channels),
            nn.ReLU(inplace=True),
            nn.Conv2d(
                out_channels,
                out_channels,
                (kernel_size[0], 1), #使用卷积核的第一维即 9 帧
                (stride, 1),
                padding,
            ),
            nn.BatchNorm2d(out_channels),
            nn.Dropout(dropout, inplace=True),
        )

10 GCN与TCN模块

每一个st-gcn是由GCN、TCN构成的，那么我们需要弄明白这个最小的构成单元的运行流程以及其原理

10.1 GCN

1	self.gcn = ConvTemporalGraphical(in_channels, out_channels,kernel_size[1])

在st-gcn中调用是这一行，传入了输入的通道层、输出的通道层的数量，最后是空间维的卷积核大小，在paper中作者说了分成3组

# st_gcn.py

...
if edge_importance_weighting:
    self.edge_importance = nn.ParameterList([
        nn.Parameter(torch.ones(self.A.size())) ## initial with one
        for i in self.st_gcn_networks
    ])
...

def forward():
    ...

    for gcn, importance in zip(self.st_gcn_networks, self.edge_importance):
    x, _ = gcn(x, self.A * importance)

    ...

#tgcn.py
# forwad
# for gcn, importance in zip(self.st_gcn_networks, self.edge_importance):
#     x, _ = gcn(x, self.A * importance)
# 注意在forward传入的A并不是单纯的self.A,而是self.A * importance
class ConvTemporalGraphical(nn.Module):
    def __init__(self,
                 in_channels,
                 out_channels,
                 kernel_size,
                 t_kernel_size=1,
                 t_stride=1,
                 t_padding=0,
                 t_dilation=1,
                 bias=True):
        super().__init__()

        self.kernel_size = kernel_size
        self.conv = nn.Conv2d(
            in_channels,
            out_channels * kernel_size,
            kernel_size=(t_kernel_size, 1),
            padding=(t_padding, 0),
            stride=(t_stride, 1),
            dilation=(t_dilation, 1),
            bias=bias)

    def forward(self, x, A):
        assert A.size(0) == self.kernel_size

        x = self.conv(x)

        n, kc, t, v = x.size()
        x = x.view(n, self.kernel_size, kc//self.kernel_size, t, v)
        x = torch.einsum('nkctv,kvw->nctw', (x, A))

        return x.contiguous(), A

上面这段代码坑其实挺多的

输入是什么？这个问题如果前面仔细看了的话会比较明白，但是对于分开代码看得人或许会出现疑问：网络的输入不是(batch_size,c,t,v,m)吗，怎么直接进行卷积了？卷积要求不是(n,c,h,w)的格式吗？如果不明白请在前面找答案，这里就不重复了。
难道这个空域的learning paramaters就是conv(x)里面的参数吗？conv的核还是1 x 1的显然与paper中3 x 1不符合呢？

为解决上面的问题，需要先看观察网络中训练的参数：

Conv1_1中的参数
A中importance的参数
A使用来进行图卷积的，所以看来gcn中卷积核的参数只能是这个Conv1_1了，但是这是怎么做到分为3组不同的权值进行计算呢？
下面将与CNN中做对比来讲解：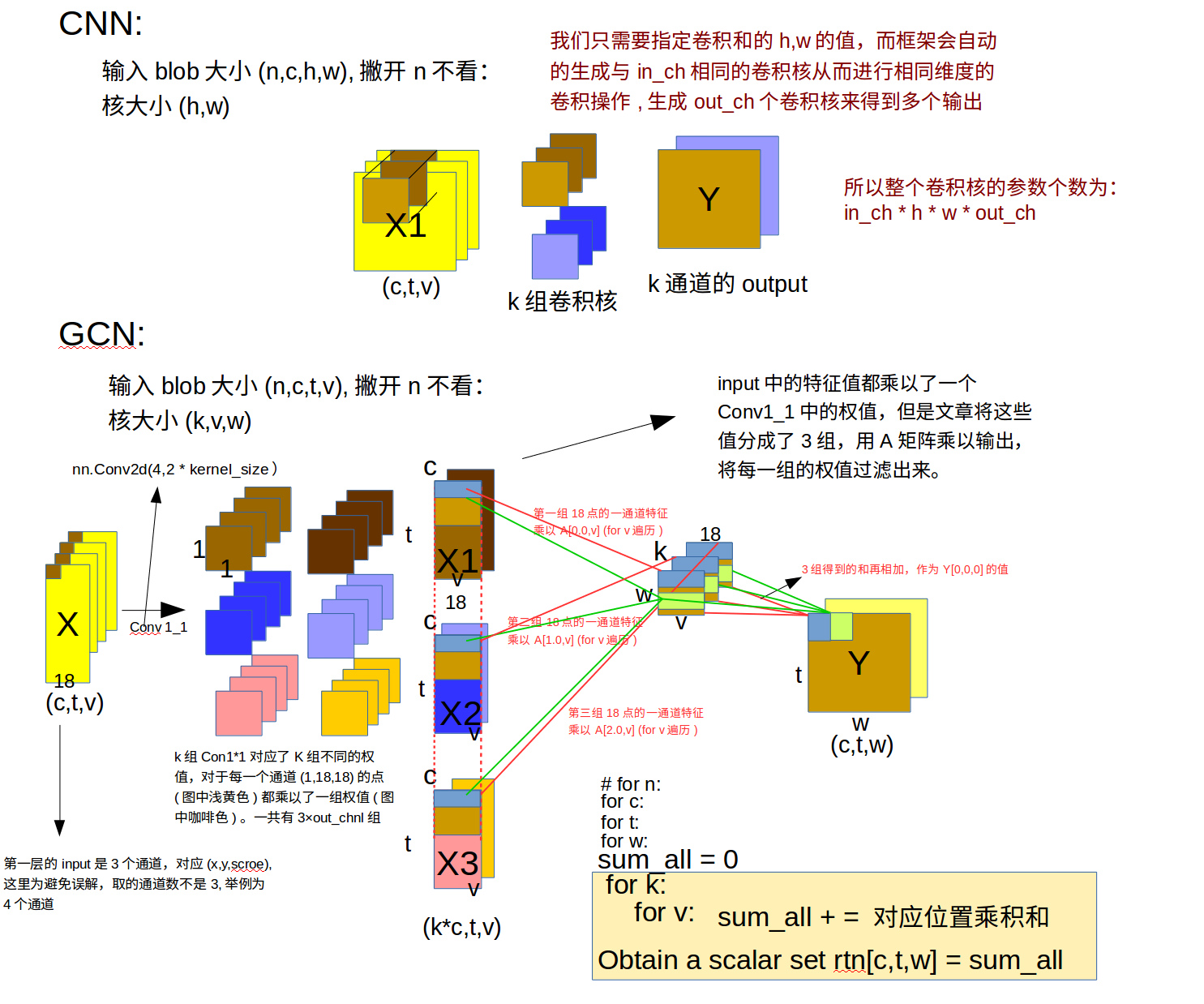
CNN GCN对比图
有了这幅图我们理解作者的意图就很容易了，X是输入的特征矩阵，为了便于说清楚原理，我们先讨论batch_size为1的情况，这样我们的输入就是(c,t,v)的特征blob，(在第一层输入c = 3)而tgcn中的conv1_1参数是(in_chanl,kernel_size*out_chanl)所以在内部会有kernel_size组blob，每个blob的c = out_chanl,每一个blob是由kernel_size×out_chanl个不同的conv1_1来实现卷积操作的，可以抽象地将这么多个卷积核分成3组，即上图中3行，每一行有out_chanl个Conv1_1卷积核。最终得到的卷积后的特征也分为3组。因为之前就将18个点分了各自的组的，所以后面又使用A矩阵来进行图卷积如下图所示
图卷积公式2
GCN图卷积公式的介绍可以参考[这篇文章][https://www.zhihu.com/question/54504471/answer/611222866]

可以简单地理解所谓图卷积就是用图卷积核($D^{-1}A$)来乘以每一个特征，可以看到图(CNN GCN对比图)中后半部分，对于每一组的18点的out_put个通道特征，我们需要用$D^{-1}A$去乘以每一个特征，具体地，C = 0时，表示取一维特征，取出18点的一维特征(蓝色框)然后使用卷积核第一行的每组参数去进行乘积加权运算(红色线标注)，一次迭代后w自增，使用卷积核第二行的每组参数去进行乘积加权运算(绿色线标注)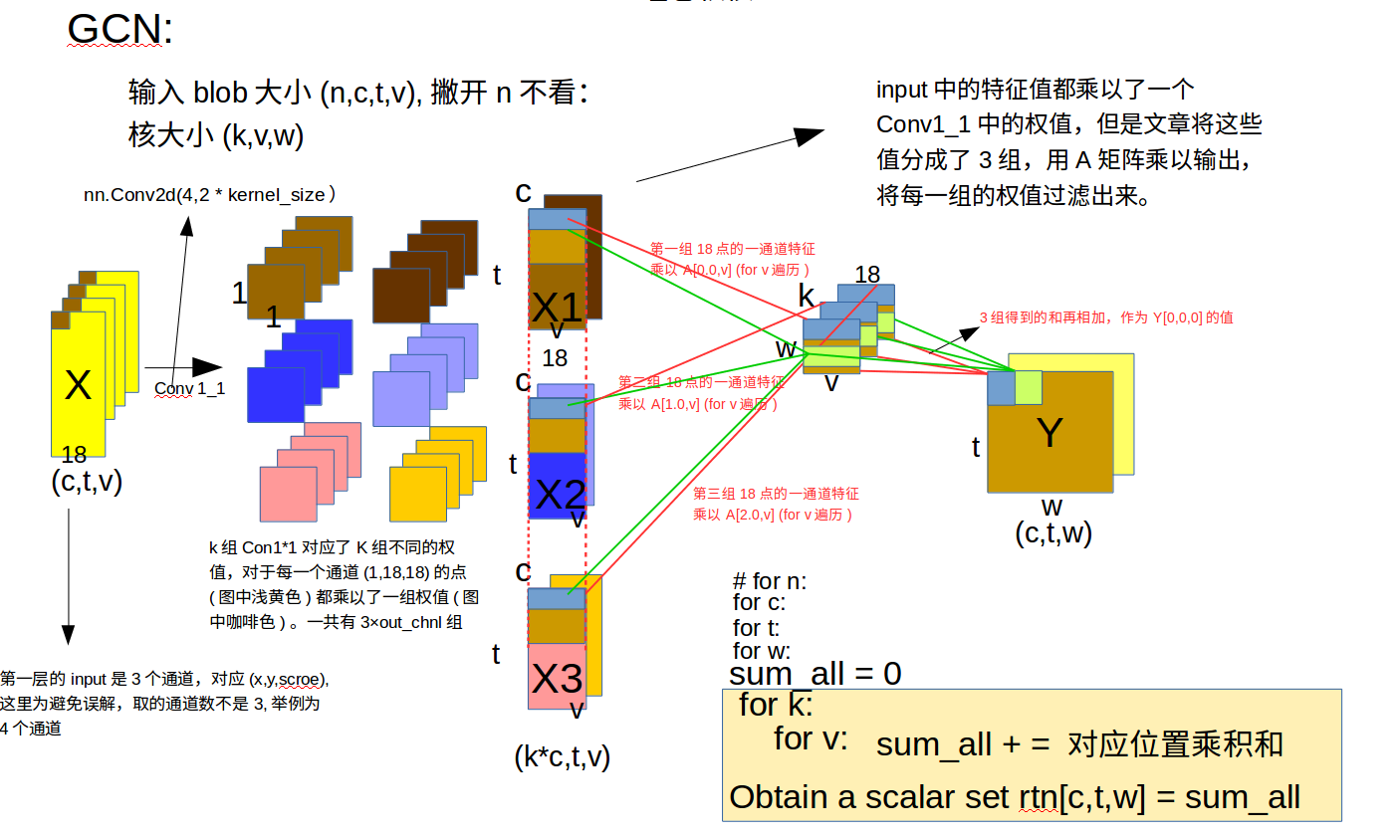
图卷积过程示意

图卷积过程示意

注意力模型

A的每一层(3,18,18)都拥有一个权值层(1,18,18),所以edge_importance是(3,18,18)对于每一A中的组，其权值都是不一样的。每一层st_gcn层也应拥有该层独立的图卷积核参数，这样照应了paper中作者所说的将节点分为3组，权值都是不同的。每一个edge_importance初始值为1,且是Parameter类型，梯度可以回流从而进行优化。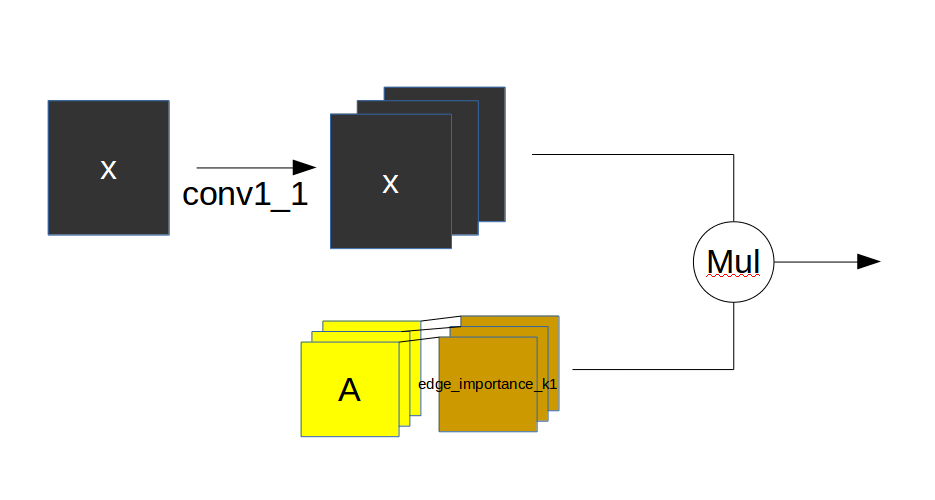
空域卷积示意图

空域卷积示意图

整个流程可以这样理解：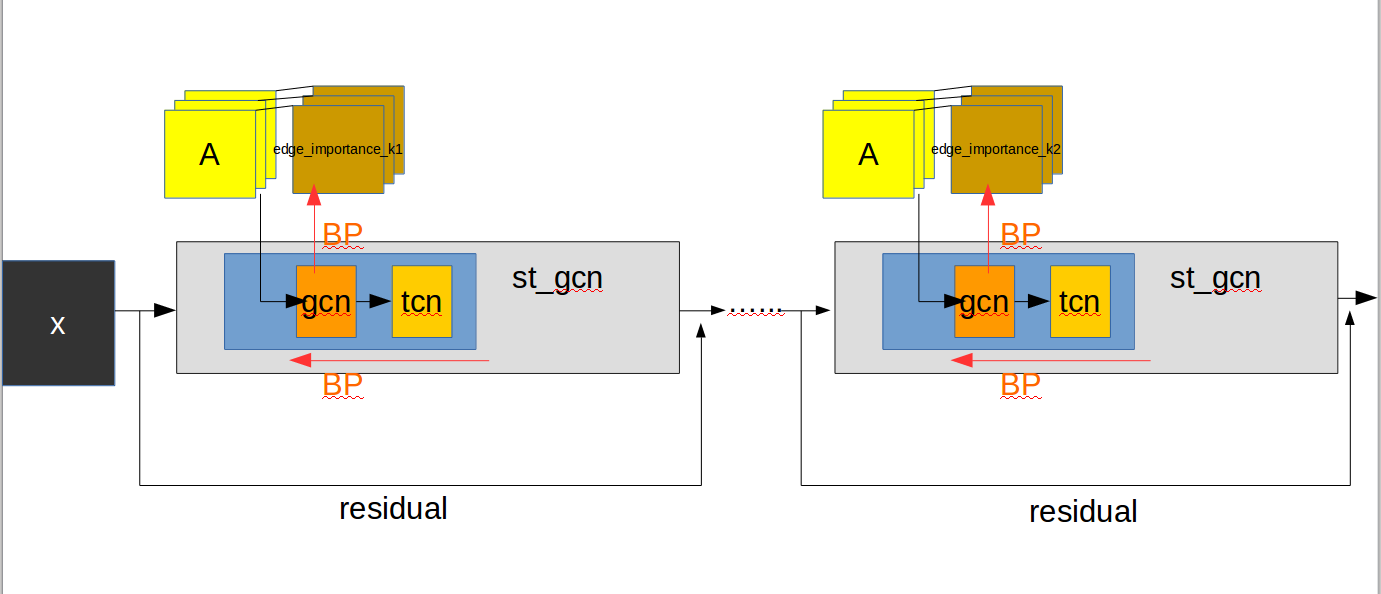
gcn过程示意图

st-gcn过程示意图

10.1.1 爱因斯坦求和约定

在ConvTemporalGraphical类中代码不多，但是原理比较难以理解，特别是在forward时作者使用了einsum的矩阵抽象乘积表达式，这让之前没有了解过这种书写格式的我费了很大功夫。对于爱因斯坦求和约定网上的博客讲的很少。
x = torch.einsum('nkctv,kvw->nctw', (x, A))这行代码的意思可以翻译为：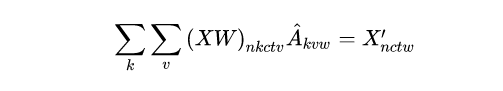
张量计算

张量计算

疑问:paper中所说的图卷积公式是这样的：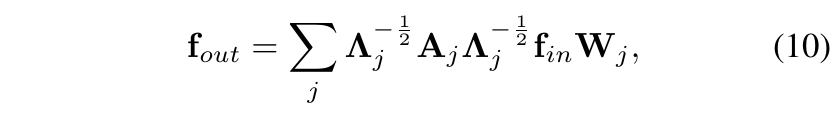
图卷积公式1

图卷积公式1

但是在源码中却是这样的：
图卷积公式2

图卷积公式2
一开始，为对这里非常不理解直到参考了GCN图卷积公式

图卷积公式2
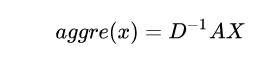
发现图卷积公式是有很多种的，源码和paper中的都可以。

疑问:对于对于公式$D^{-1}AX$来说那应该是A在左边X在右，但是代码中x = torch.einsum('nkctv,kvw->nctw', (x, A))却是在反的，计算会出错吗？

解答爱因斯坦求和不是矩阵的运算，而是对应的元素的线性变换，在代码中是与先后无关的。这段求和可以这样理解：
eins求和

eins求和

为了更好的理解einsum在这里举一个例子：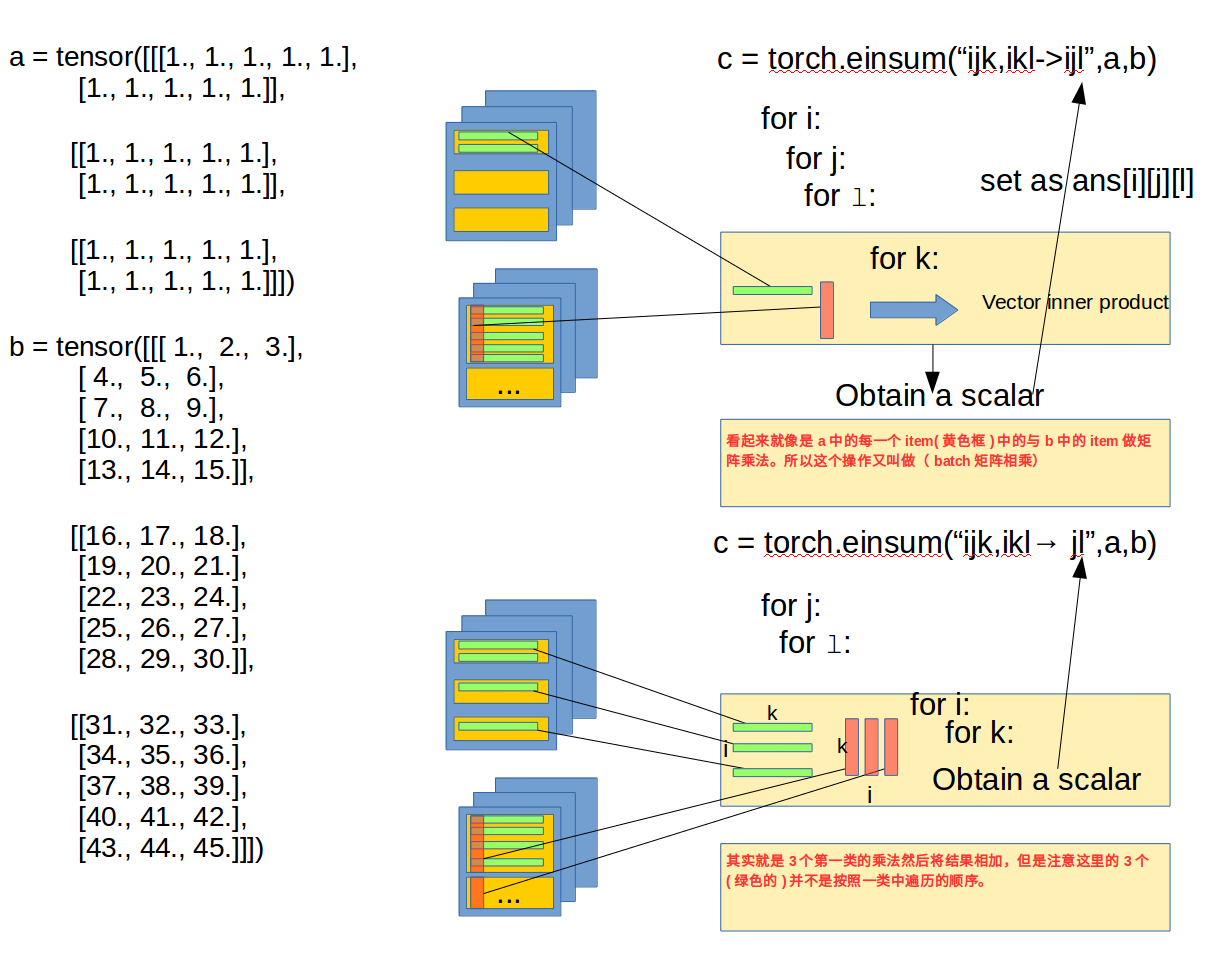
eins求和

eins例子
这里也再次强调下如果改为B = torch.einsum("ikl,ijk-> ijl",b,a)即B在前A在后，其结果是一样的,这里不论顺序，只要维度能匹配上就会按照正确顺序进行内积，其实从代码角度也可以理解，在第二轮计算和时是没有管谁前谁后的，就是k维度的遍历，然后依次加起来。

eins代码角度分析
综上，einsum中是不用在意变量的顺序的

10.2 TCN

在GCN后面紧跟着就是TCN的模块，该模块让网络在时域中进行特征的提取，类似与LSTM，GCN的输出是一个(n,c,t,w)的blob，在TCN中可以简单的理解为和CNN的输入格式一样。

self.tcn = nn.Sequential(
            nn.BatchNorm2d(out_channels),
            nn.ReLU(inplace=True),
            nn.Conv2d(
                out_channels,
                out_channels, # 不改变chanl值
                (kernel_size[0], 1),
                (stride, 1), # stride可以控制t域的缩小，可当做poolling操作
                padding,
            ),
            nn.BatchNorm2d(out_channels),
            nn.Dropout(dropout, inplace=True),
        )

一个TCN层由下面组成

BN 模块
Conv2d 模块
BN 模块
Dropout 模块
BN的用法参考我之前的BN的文章。这里主要就是Conv2d的卷积模块，卷积核大小为(9,1)，

在10.1节中介绍了GCN，在GCN中只对每一帧的空间信息进行卷积，将18个特征分为3组置于不同的权值相当于卷积核大小为(3,1)的卷积操作(3个权值取加权平均置于目标位置)，其输出仍然是一个(n,c,t=300,v=18)的blob。

在TCN的模块就是对T的卷积了，这部分比gcn容易理解，就是正常的卷积操作，对于同一个节点在不同t下的特征的卷积。

至此我们就完成了st-gcn的模型框架的分析，下面是一些实验结果：

11 结果

数据集：hmdb51
首先使用OpenPose对视频进行pose节点的预测，将输出进行格式化输出到json文件中
节点json文件

节点json文件OpenPose 的运用可以参考之前一篇专门将OpenPose的文章。

使用st_gcn进行数据的读入

def get_data_from_json(self,output_path):
    FRAME_HEIGHT = 256
    FRAME_WIDTH = 360
    with open(output_path, 'r') as f:
        video_info = json.load(f)

    data_numpy = np.zeros((3, 300, 18, 2))
    for frame_info in video_info['data']:
        frame_index = frame_info['frame_index']
        if frame_info["skeleton"] == None:
            continue
        for m, skeleton_info in enumerate(frame_info["skeleton"]):
            if m >= 2:
                break
            pose = skeleton_info['pose']
            score = skeleton_info['score']
            data_numpy[0, frame_index, :, m] = np.array(pose[0::2]) / FRAME_WIDTH
            data_numpy[1, frame_index, :, m] = np.array(pose[1::2]) / FRAME_HEIGHT
            data_numpy[2, frame_index, :, m] = score
    data_numpy[0:2] = data_numpy[0:2] - 0.5
    data_numpy[0][data_numpy[2] == 0] = 0
    data_numpy[1][data_numpy[2] == 0] = 0
    return data_numpy[np.newaxis,:]

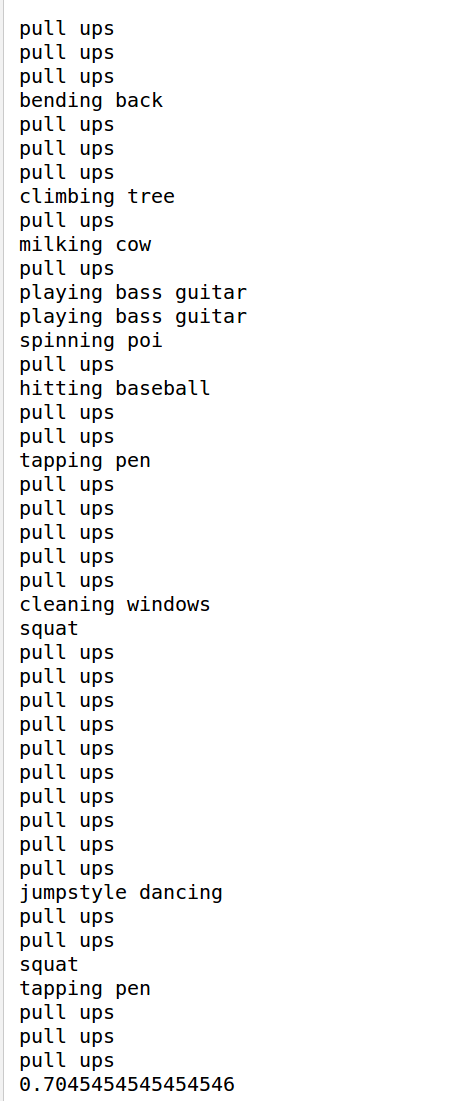
使用网络对其进行预测，这里我首先测试对于一个类，st-gcn的预测精度是多少,测试的类别是pull_up类。

def predic(self,json_file_path):
    filenames = os.listdir(json_file_path)
    label_name=[]
    with open('./resource/kinetics_skeleton/label_name.txt', 'r') as f:
        for line in f:
            label_name.append(line.strip('\n'))
    ret = []
    # 对每一个待检测的json文件进行预测
    for fn in filenames:
        self.model.eval()
        json_path = os.path.join(json_file_path,str(fn))
        data = self.get_data_from_json(json_path)
        data_tensor = torch.from_numpy(data)
        data_tensor = data_tensor.float().to(self.dev)
        del(data)
        with torch.no_grad():
            output = self.model(data_tensor)
            output = output.data.cpu().numpy()
            max_probablity_index = output.argmax(axis = 1)
        # label_name = np.loadtxt('./resource/kinetics_skeleton/label_name.txt',dtype=str,delimiter=None,)
        # print(max_probablity_index)
        ret.append(label_name[int(max_probablity_index)])
        # print(label_name[int(max_probablity_index)])
    cnt = 0
    for it in ret:
        if it == 'pull ups':
            cnt +=1
    print(ret)
    print(cnt/len(ret))

最终结果为
预测结果

预测结果

参考

GCN_smi
st-gcn论文解析
 对角矩阵